A flowchart proof brainlycraigslist buena vista: This investigation explores the unexpected intersection of mathematical proof techniques, online learning platforms, and a hypothetical geographical context. We examine the use of flowchart proofs, a visual method for demonstrating geometric theorems, and consider the potential—and pitfalls—of sourcing information from online communities like Brainly and Craigslist. The case study focuses on a fictional Buena Vista, highlighting how these disparate elements might converge in a real-world scenario.
The study will delve into the strengths and weaknesses of using Brainly and Craigslist for academic research, emphasizing the importance of verifying information obtained from these sources. We’ll then construct a hypothetical problem related to Buena Vista’s geography, demonstrating how a flowchart proof can provide a clear and logical solution. Finally, we will discuss the benefits of integrating visual proof methods, such as flowcharts, into educational programs.
Flowchart Proofs, Online Resources, and Buena Vista: A Flowchart Proof Brainlycraigslist Buena Vista
This article explores the application of flowchart proofs in a geometric context, examining their utility alongside online resources like Brainly and Craigslist. We will then analyze the relevance of these tools within a hypothetical Buena Vista setting, focusing on the accessibility and reliability of information obtained from these platforms.
Flowchart Proofs and Their Applications
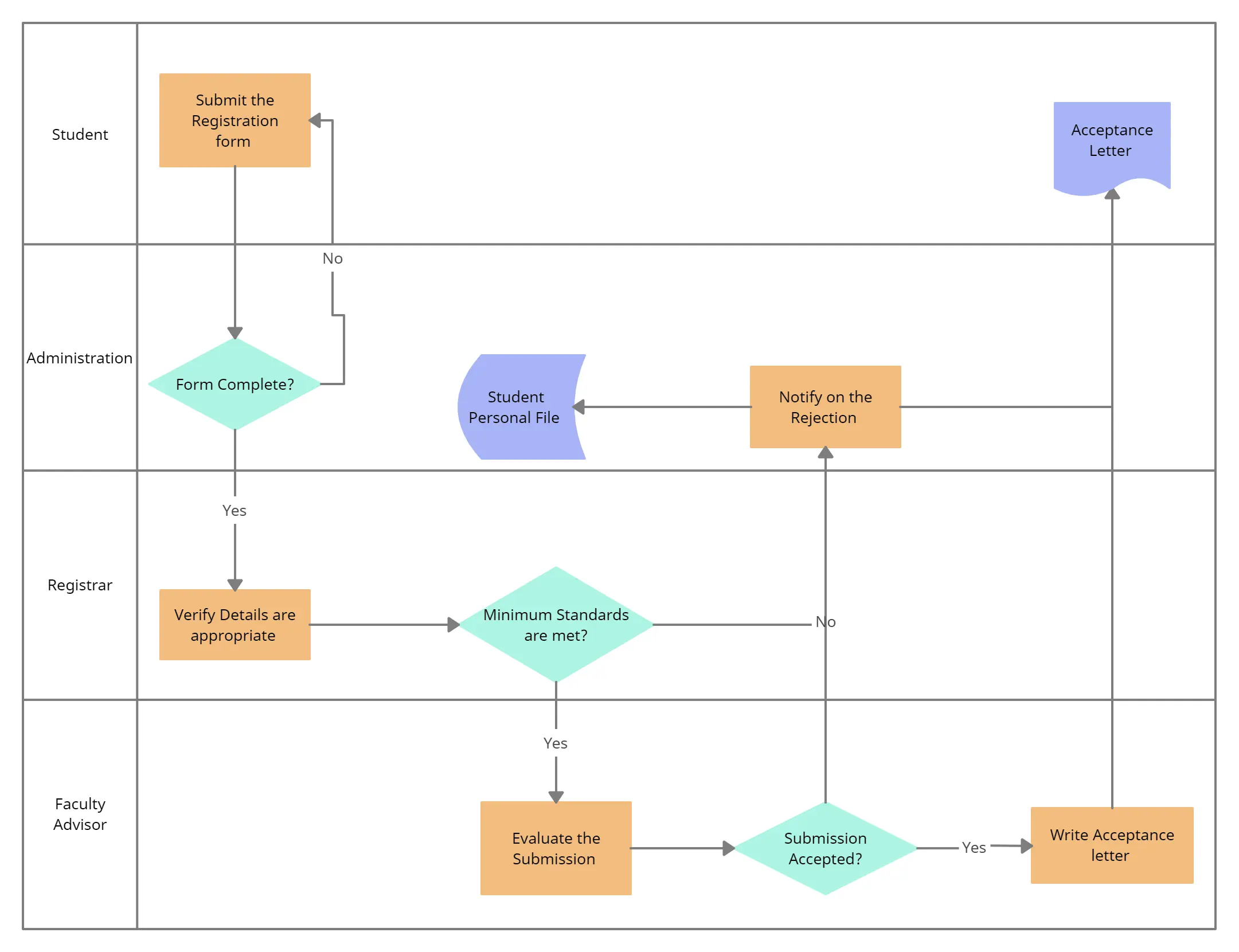
Flowchart proofs offer a visual and structured method for demonstrating mathematical theorems. They utilize a series of interconnected boxes representing logical steps and conclusions, leading to a clear and concise presentation of the proof. Each box typically contains a statement or reason, linking geometric properties and postulates to the final theorem.
Examples of theorems demonstrable using flowcharts include the Isosceles Triangle Theorem (proving equal angles opposite equal sides), the Pythagorean Theorem (relating the sides of a right-angled triangle), and theorems concerning parallel lines and transversals (demonstrating congruent or supplementary angles).
Constructing a flowchart proof involves breaking down the theorem into a sequence of logical steps. Each step is represented in a box, with justifications (reasons) linked using arrows to show the logical flow. The process starts with given information and proceeds through deductive reasoning until the theorem is proven.
A flowchart proof for the Pythagorean Theorem would begin with the given right-angled triangle and its sides. It would then involve applying the area formulas for squares constructed on each side, leading to the equality a² + b² = c², where ‘a’ and ‘b’ are the legs and ‘c’ is the hypotenuse. Each step would be justified using geometric postulates or previously proven theorems.
Do not overlook explore the latest data about fort smith craigslist free stuff.
Flowchart proofs provide a clear visual alternative to traditional written proofs, offering a more accessible and easily understandable representation for many learners. They highlight the logical progression of the argument, making the reasoning process transparent.
Brainly and Craigslist: A Comparative Analysis
Brainly and Craigslist represent vastly different platforms for information sharing. Brainly functions as a peer-to-peer learning community, where users can ask and answer questions across various subjects, including mathematics. Craigslist, primarily a classifieds website, offers a less structured environment for information exchange.
While Brainly offers a dedicated space for mathematical inquiries, the accuracy of answers relies on the expertise and honesty of the contributors. Craigslist, on the other hand, is not specifically designed for academic support, and finding reliable mathematical resources there would be highly challenging.
Verifying information on both platforms requires critical evaluation. On Brainly, checking multiple responses and looking for consensus can improve reliability. On Craigslist, the lack of moderation and quality control necessitates extreme caution and independent verification from trusted sources.
Using information from Craigslist for academic purposes carries significant risks. The lack of oversight increases the likelihood of encountering inaccurate, incomplete, or even plagiarized content. This could lead to academic penalties and compromise the integrity of one’s work.
| Feature | Brainly | Craigslist |
|---|---|---|
| Purpose | Peer-to-peer learning | Classifieds and community listings |
| Content Reliability | Moderately reliable (user-dependent) | Low reliability |
| Accuracy Verification | Requires critical evaluation | Extremely difficult |
| Risk for Academic Use | Moderate (potential for inaccurate answers) | High (risk of plagiarism and inaccurate information) |
Buena Vista Context and Relevance, A flowchart proof brainlycraigslist buena vista
Imagine Buena Vista, a coastal town with a need to calculate the optimal placement of a new pier based on tidal patterns and shoreline measurements. A flowchart proof could be used to demonstrate the geometric principles involved in determining the pier’s location, ensuring its structural integrity and safety.
For instance, a problem involving determining the shortest distance between two points on the coast (A and B) across a river could be solved using a flowchart proof. This might involve reflecting one point across the river to create a congruent triangle, proving that the shortest distance is a straight line connecting the reflected point to the other point.
A hypothetical situation could involve a local contractor in Buena Vista needing to calculate the area of an irregularly shaped plot of land for a construction project. They might find relevant formulas or examples on Brainly, but need to carefully verify the information before applying it.
- Local library resources (geometry textbooks, online databases)
- High school or community college mathematics courses
- Online educational platforms (Khan Academy, Coursera)
- Consultations with local engineers or surveyors
A hypothetical educational program in Buena Vista could integrate flowchart proofs into its geometry curriculum by incorporating hands-on projects, such as designing and building models to illustrate geometric theorems. This approach would combine theoretical understanding with practical application, fostering deeper comprehension.
Visual Representation and Communication

A flowchart proof visually represents a mathematical argument through a series of connected boxes. Each box contains a statement (a step in the proof) and a justification (the reason why that step is valid). Arrows connect the boxes, showing the logical flow from the given information to the conclusion. The structure is hierarchical, starting with given statements and leading step-by-step to the final theorem.
Interpreting a flowchart proof involves following the arrows from the initial given statements. Each box’s statement and justification should be carefully examined to understand the logical connection between steps. The overall flow should lead to a clear and unambiguous conclusion.
Flowcharts offer significant advantages for visualizing mathematical proofs. They make the logical structure clear and easy to follow, particularly for complex proofs. This visual representation improves understanding and retention, compared to traditional written proofs, which can sometimes appear dense and abstract.
Flowcharts, when compared to written proofs, often enhance communication of mathematical concepts, particularly for visual learners. The visual flow aids comprehension, reducing the cognitive load required to understand the reasoning behind each step. The clear structure reduces ambiguity and enhances the overall clarity of the proof.
To illustrate a specific step, consider a box stating “Angles A and B are congruent because they are vertical angles.” A visual aid could show two intersecting lines with angles A and B clearly marked and labeled as vertical angles, highlighting their equal measures.
In conclusion, while online resources like Brainly and Craigslist offer potential avenues for accessing information, critical evaluation remains paramount. The application of flowchart proofs, with their clear visual structure, offers a powerful tool for solving complex problems and communicating mathematical concepts effectively. The hypothetical Buena Vista scenario underscores the potential for integrating these methods into diverse educational settings, fostering a deeper understanding of mathematical principles and promoting critical thinking skills.
Further research could explore the broader implications of utilizing online resources in conjunction with visual proof techniques across various disciplines.

